High temperature RF-SQUID consists of a superconducting loop, which has one Josephson Junction (JJ). For the operation of the RF-SQUID there is a restriction that the inductance parameter β_L=2πI_CL_S/Φ₀ is in the range of 1~3, where I_C is the critical current of JJ, L_s is the SQUID inductance and Φ₀ is the flux quantum. However, since the both ends of the JJ of RF-SQUID are shorted by a superconducting loop, it is necessary to cut the loop to evaluate the I_C. Therefore, we proposed a method to nondestructively measure the I_C of the RF-SQUID using another SQUID magnetometer ^[1].

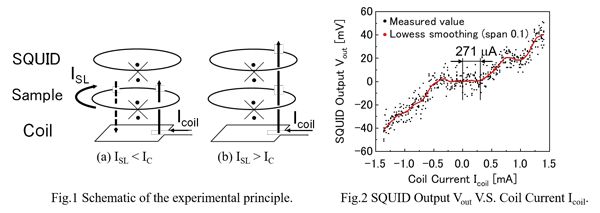
 Fig.1 shows the experimental set-up. It consist of an RF-SQUID magnetometer (made by Jülicher SQUID GmbH), a superconducting ring sample, and a coil for applying a magnetic field with an internal dimensions of 3.3 mm × 3.3 mm and a width of 0.35 mm, which were placed in a coaxial stacked configuration. The coil was appressed against the ring sample, and the distance between the surfaces of the ring sample and the SQUID was 4.6 mm. We suppose that a shielding current I_SL in the sample is induced when applying a magnetic field from the coil. Fig.1 (a) shows the principle of the measurement. When the I_SL is below the I_C of the ring sample, the SQUID does not respond to the field because of the induced shielding current I_SL, which cancels the applied magnetic field. When the applied magnetic field is increased, as shown in Fig.1 (b), the shielding current I_SL exceed the I_C and then the junction of the sample becomes a normal conducting state. As a result, the magnetic flux threads into the ring sample, and the SQUID responds. Fig.2 shows the experimental results. The SQUID output V_out increased when the coil current I_coil exceeded 271 µA. The induced shielding current I_SL in the ring sample could be expressed by a formula, I_SL = α(L_coil×L_SL)^1/2×I_coil / L_SL. Here α is the coupling coefficient between the coil and the sample, and L_coil and L_SL are their inductances. By cutting the sample and measuring the I_C, the α could be determined. After determining the α, we could estimate the I_C of unknown ring samples by the formula.

[1] M. J. Ferrari et al., J. Low Temp. Phys. 94 pp. 15-61 (1994).

Keywords: RF-SQUID, Critical current, Nondestructive evaluation, HTS