We formulate an efficient scheme to perform Migdal-Eliashberg calculation considering the retardation effect from first principles^[1]. While the conventional approach requires a huge number of Matsubara frequencies, we show that the intermediate representation (IR) of the Green’s function^[2] and the sparse sampling method^[3] dramatically reduce the numerical cost to solve the linearized gap equation. Without introducing any empirical parameter such as μ^*, we demonstrate that we can reproduce the experimental superconducting transition temperature of elemental Nb (~ 10 K). The present result indicates that our approach has a superior performance for many superconductors for which T_c is lower than the order of 10 K. Our scheme based on IR reduces the computation time cost and memory footprint by 20 times, compared to the conventional method using 4000 Matsubara frequencies.

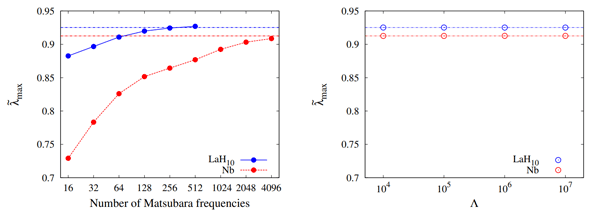
Fig. (a) Eigenvalue of Eliashberg gap equation lmax vs the number of Matsubara frequencies for Nb (red) and LaH10 (blue) at 250 Gpa. (b) lmax vs controlling parameter L of IR. The results using IR are consistent with the results obtained with a sufficient large number of Matsubara frequencies. The horizontal dash-dotted lines in (a) and (b) indicate the converged result for Nb (red) and LaH10 (blue) at 250 Gpa.

[1] T. Wang, T. Nomoto, Y. Nomura, H. Shinaoka, J. Otsuki, T. Koretsune and R. Arita, arXiv:2004.08591
[2] H. Shinaoka, J. Otsuki, M. Ohzeki and K. Yoshimi, Phys. Rev. B 96, 035147 (2017)
[3] J. Li, M. Wallerberger, N. Chikano, C.-N. Yeh, E. Gull, and H. Shinaoka, Phys. Rev. B 101, 035144 (2020)

Keywords: Electron-phonon coupling, Migdal-Eliashberg theory, First-principles calculation