PC3-7
Classifying Superconductivity in Magic-Angle Twisted Bilayer Graphene Superlattices
Dec.1 16:45-17:00 (Tokyo Time)
M.N. Miheev Institute of Metal Physics, Russian Academy of Sciences, 18 S. Kovalevskoy St, Ekaterinburg 620108, Russia1
Ural Federal University, 19 Mira St., Ekaterinburg, 620002, Russia2
Robinson Research Institute, Victoria University of Wellington, 69 Gracefield Rd., Lower Hutt 5010, New Zealand3
Department of Applied Physics, Aalto University, P.O. Box 15100, FI-00076 Aalto, Finland4
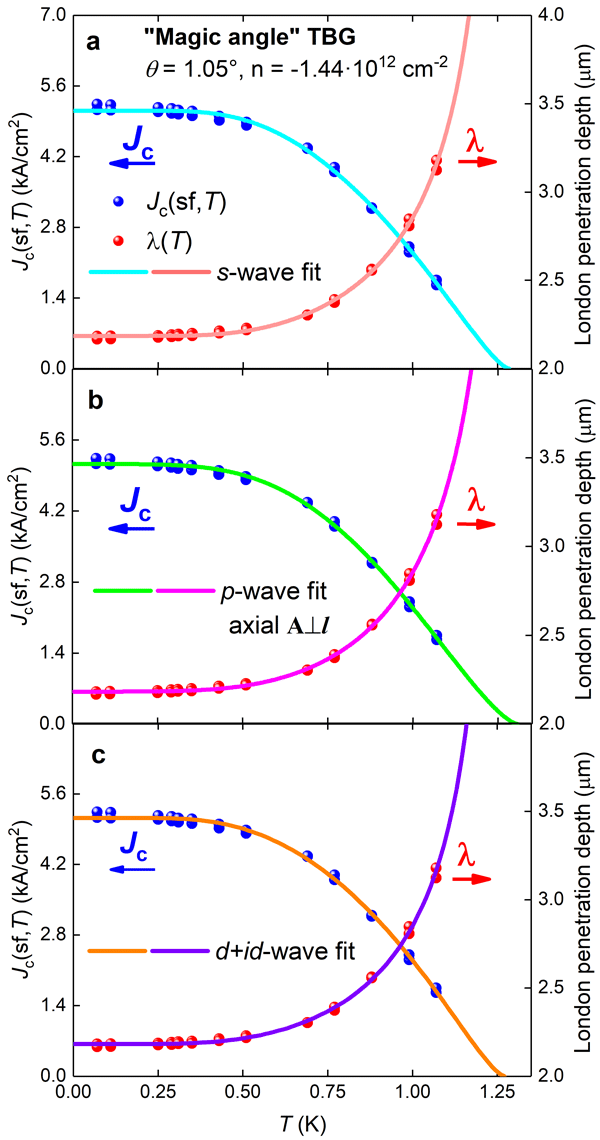
Cao et al [1] discovered the superconducting state in bilayer graphene structures where single atomic layers of graphene are stacked and then twisted at angles q forming Moiré superlattices. Here we deduce the London penetration depth, λ(0), the superconducting energy gap, Δ(0), the relative jump in electronic specific heat at transition temperature, ΔC/C, and superconducting coherence length, ξ(0), in bilayer graphene Moiré superlattices twisted at θ = 1.05°, 1.10° and 1.16° by analyzing the temperature dependence of the upper critical field Bc2(T) and the self–field critical current Jc(sf,T) within currently available models – all of which start from phonon-mediated BCS theory – for single– and two–band s–, d–, p– and d+id–wave gap symmetries. Extracted superconducting parameters show that only s–wave (Fig. (a)) and a specific kind of p–wave (Fig. (b)) symmetries are likely to be dominant in bilayer graphene Moiré superlattices. Despite that Jc(sf,T) fit to d1+id2–wave gap model has a good quality (Fig. (c)), deduced gap–to– critical temperature ratios, 5.9 and 3.3, are too different as from the weak-coupling limit of 4.28 (for this symmetry), as well as from each other. This makes it very unlikely that this gap symmetry can exhibit in magic–angle twisted bilayer graphene superlattices. More experimental data is required to distinguish between the s– and remaining p–wave symmetries as well as the suspected two–band superconductivity in these 2D superlattices.
[1] Y. Cao, et al 2018 Unconventional superconductivity in magic–angle graphene superlattices Nature 556 43-50
Fig. The self–field critical current density, Jc(sf,T), for sample M2 (θ = 1.05°) from the work of Cao et al [1] and a fit of the data to three single-band models. (a) s–wave fit; (b) p–wave axial A⊥l fit; (c) d+id–wave fit.
Keywords: Magic-Angle Twisted Bilayer Graphene, Superconducting Gap Symmetry, London Penetration Depth, Superconducting Coherence Length