Self-rectifying flux pumps are devices that rectify an asymmetric ac input current to generate a dc current over a superconducting load [1]. They are capable of delivering large currents at modest voltages [2] without the need for direct electrical and thermal connection between the superconducting load and an ambient temperature power supply. Together with the absence of moving parts and relatively few components, they may be an attractive alternative to conventional power supplies or other types of flux pumps [3], [4].

Recently, we have developed effective circuit models of self-rectifying flux pumps that are implemented and solved within the Simulink package in MatLab. We consider the electrical and magnetic circuits involved and treat the resistivity of the superconducting components, ρ_SC, as a non-linear function of current density, J;

 ρ_SC = [ E₀ / J_c ] * [ J / J_c ]^n-1

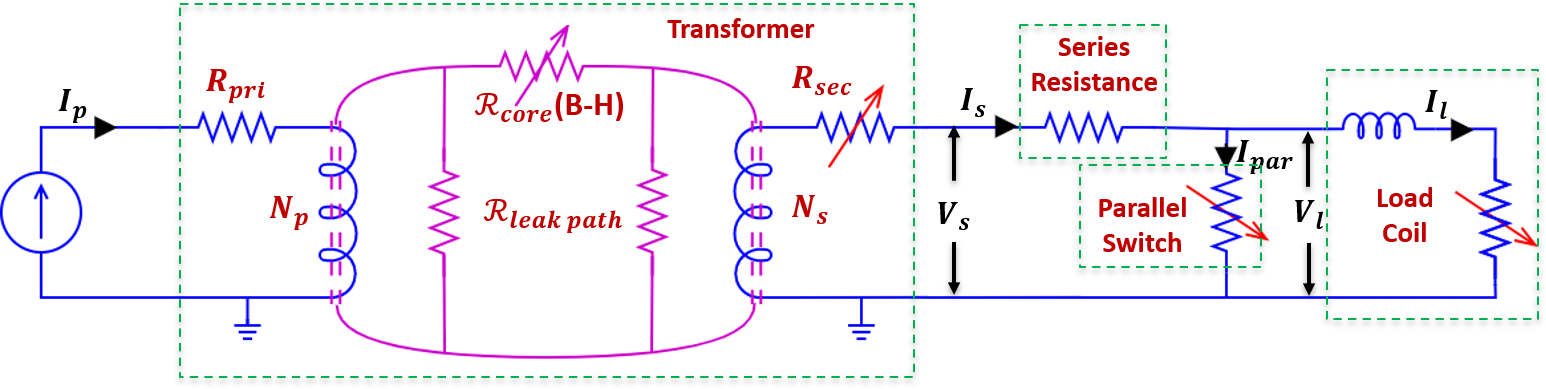
Where E₀= 1 μV.cm^-1 is the customary electric field at which the critical current density of a superconductor, J-_c, is defined. n is obtained from fitting characteristic experimental data [5] and captures the steepness of the resistivity increase as J exceeds J_c. A simple example of an effective circuit used in this work is shown in Figure 1.

In this presentation, we discuss our modelling approach and the comparison between its results and experimental data from a dedicated test rig and from data in the literature [1], [2]. From this comparison, we argue that the effective circuit model describes the essential function of self-rectifiers. As such, we show how this modelling approach provides a tool for understanding interplay of the components of the flux pumps and how it can aid in the optimization of their design.

Several additional physical effects, such as dynamic resistance, magnetic field and temperature, can be readily included within the modelling approach and are considered necessary to more fully capture all available experimental data.

References:
[1] J. Geng and T. A. Coombs, “An HTS flux pump operated by directly driving a superconductor into flux flow region in theE–Jcurve,” Supercond. Sci. Technol., vol. 29, no. 9, p. 095004, Jul. 2016, doi: 10.1088/0953-2048/29/9/095004.
[2] J. Geng, C. W. Bumby, and R. A. Badcock, “Maximising the current output from a self-switching kA-class rectifier flux pump,” Supercond. Sci. Technol., vol. 33, no. 4, p. 045005, Apr. 2020, doi: 10.1088/1361-6668/ab6957.
[3] J. Geng, R. A. Badcock, and C. W. Bumby, “A Wireless Rectifier for Inductively Energizing High Direct-Current High-Temperature Superconducting Magnets,” IEEE Transactions on Industrial Electronics, vol. 68, no. 4, pp. 3273–3281, Apr. 2021, doi: 10.1109/TIE.2020.2982095.
[4] J. G. Storey, A. E. Pantoja, Z. Jiang, R. A. Badcock, and C. W. Bumby, “Optimizing Rotor Speed and Geometry for an Externally Mounted HTS Dynamo,” IEEE Transactions on Applied Superconductivity, vol. 29, no. 5, pp. 1–5, Aug. 2019, doi: 10.1109/TASC.2019.2903038.
[5] S. C. Wimbush and N. M. Strickland, “A Public Database of High-Temperature Superconductor Critical Current Data,” IEEE Transactions on Applied Superconductivity, vol. 27, no. 4, pp. 1–5, Jun. 2017, doi: 10.1109/TASC.2016.2628700.

Acknowledgements:
This work was supported by the New Zealand Ministry of Business, Innovation and Employment (MBIE) under contract no. RTVU1707 and Strategic Science Investment Fund “Advanced Energy Technology Platforms” contract RTVU2004.

Figure caption: An example of a simple effective circuit used to model the response of a transformer-rectifier flux pump. The superconducting components, “R_sec”, “Parallel switch” and “Load coil” are modelled using custom non-linear functions.

Keywords: Flux pump, Self rectifier, Modelling, Self regulating