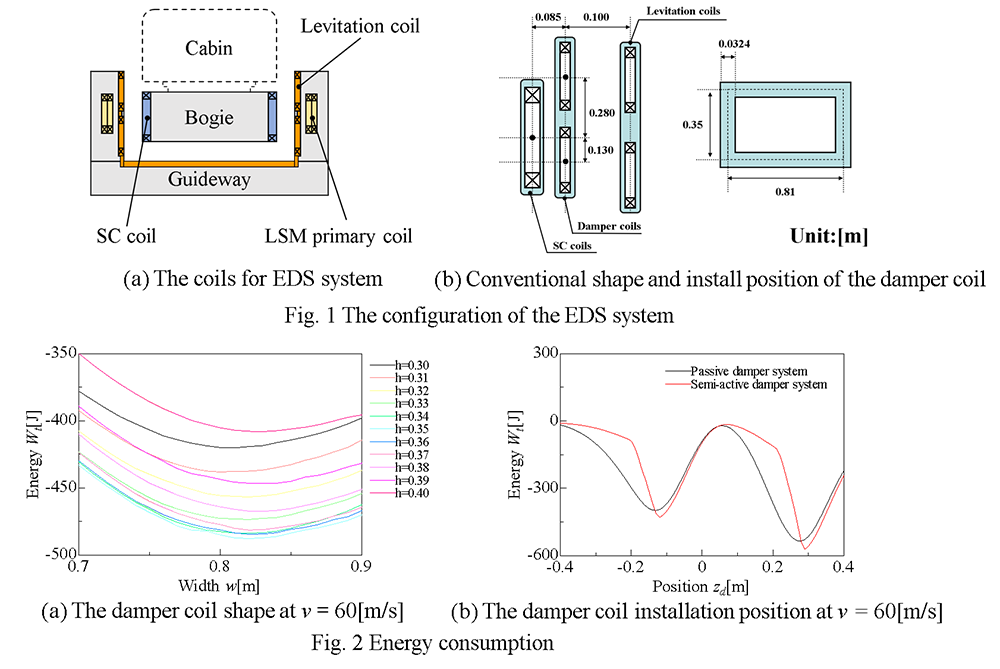
High speed magnetically levitation systems are developed for transportation. The principle of the electrodynamic suspension system (EDS) is electromagnetic induction, and this system is used for levitation and guidance[1]. This system has basically no damping factor against the vertical oscillation of the bogie. Thus, the passive damper system is introduced. Fig.1 shows the configuration of the EDS system. The damper coil current of this system is delayed by its self-inductance against oscillation of the bogie. Thus, there are periods that the damper coil increases oscillation of the bogie. To solve this problem, the semi-active damper system is introduced. The damper coils are switched according to the oscillation velocity of the bogie and the magnetic force generated by the damper coils. As a typical application of the EDS system, this paper discusses about the JR Maglev. The operation velocity of the JR Maglev is v = 120[m/s]. At low velocity such as the velocity v = 60, 80[m/s], the damping factor is small. Previous studies have adopted the optimized damper coil at the v = 120[m/s][2]. In this study, the optimal shape and installation position of the damper coil at the low velocity is studied by numerical analysis.

The levitation force is generated by the superconducting (SC) coil attached to the bogie and the levitation coil on the ground in JR Maglev. The eight-figure null-flux connection is used for the levitation coils. When the bogie passes in front of the eight figure coils, the levitation force is generated to the bogie. The electric circuit model is established to simulate the motion of the bogie in this EDS system[3].
The shape and installation position of the damper coil is discussed by energy consumption. The bogie is forced by the virtual external force to oscillate in the vertical direction based on the basic oscillation of the EDS system with moving the running direction at the constant velocity v = 60, 80[m/s]. The energy worked on the bogie by the external force indicates the damping factor. When this energy is negative, the damper coil works to decrease the oscillation of the bogie. Therefore, when the energy takes negative peak, the damper coil is optimal one[4].

In the optimal shape damper coil, the width of the damper coil is considered at the width w = 0.7 - 0.9[m]. the reason is that, according to previous research, the width of the damper coil indicated as optimal around the w = 0.8[m][4]. The height of the damper coils is considered at h = 0.30 - 0.40 [m]. Also, in the semi-active damper system, the insertion resistance of the damper coil is Rs = 0.03 - 0.08 [Ω]. The weight of the damper coil is 10.31 [kg]. Fig.2 (a) shows energy consumption of the damper coil shape at the v = 60[m/s]. From simulation results, in passive damper system, the optimal shape of the damper coil at the v = 60[m/s] is the h = 0.36[m], the w = 0.90[m] and at the v = 80[m/s] is the h = 0.35[m], the w = 0.86[m]. In semi-active damper system, that at the v = 60, 80[m/s] is the h = 0.35[m], the w = 0.82[m]. The optimal height of damper coil varies only 0.01[m]. This height is almost the same as the height of levitation coil. The optimal width of damper coil at v = 60[m/s] in passive damper system is 0.08[m] larger than in semi-active damper system and 0.04[m] larger than at the v = 80[m/s]. In conclusion, at the low velocity range, the optimal height of the damper coil is almost independent of the damper systems and the velocity. The optimal width of the damper coil varies depending on the damper systems and the velocity.

Optimal installation position of the damper coils on the bogie is discussed. The shape of damper coil is the damper coil optimized in the earlier parts of this paper. four damper coils are installed on each side of the bogie as the installation position of the damper coils -0.40 - 0.40 [m]. Fig. 2(b) shows the energy consumption of the damper coil installation position at the v = 60[m/sec]. From Fig. 2(b), there are two position where the energy takes negative peak. When the damper coils are installed in front of the upper or lower levitation coils, the damping factor is large. Thus, there are two optimal installation positions of the damper coils. In passive damper system, the optimal installation positions of the damper coil are z_d = -0.13, 0.28[m] at the v = 60[m/s] and z_d = -0.14, 0.27[m] at the v = 80[m/s]. In the semi-active damper system, these are z_d = -0.12, 0.29[m] at the velocity v = 60, 80[m/s]. The optimal installation positions at v = 60[m/s] in passive damper system are 0.02[m] larger then in semi-active damper system and 0.01[m] larger than at the v = 80[m/s]. In conclusion, at the low range velocity, in passive damper system, the optimal installation positions of the damper coil depend on the velocity. In semi-active damper system, these positions of the damper coil are independent of the velocity and higher than in passive damper system.

Reference
[1]A.Seki, J.Kitano and S.Miyamoto, “Dynamics of the bogie of a maglev system with guideway irregularities”, IEEE Trans. on Magnetics vol.32, No.5, pp5043-5045, 1996.

[2]R.Betsunoh, and S.Ohashi, “Improvement of the Damping Factor at Low Speed in Electrodynamic Suspension System for the JR Maglev”, 2021 J. phys.:Conf. Ser. 1975 012031

[3]S.Ohashi and T.Ueshima, “Control Method of the Semi-Active Damper Coil System in the Superconducting Magnetically Levitated Bogie Against Vertical and Pitching Oscillation”, IEEE Trans. on Magn. vol.48, No.11, pp4542-4544, 2012.

[4]S. Ohashi, “Weight Reduction of the Damper Coils in the Superconducting Magnetically Levitated Bogie”, IEEE Trans. on Magn. Vol. 54, no. 11, 2018.

Keywords: Electro-dynamic Suspension, Damping, Magnetic Levitation, Numerical Simulation