Today, DC SQUIDs are extensively used in commercially applications as sensitive magnetometers such as microscopy, readout electronics, nondestructive test, biomagnetism applications. [1]DC SQUID’s voltage response against external applied magnetic field is non-linear, this situation may cause difficulties in application and limit the dynamic range of sensor. As a result, researchers tend to investigate DC SQUID based circuits, which is more linear than conventional DC SQUIDs (Bi-SQUID, arrays of SQUIDs, …, etc.). Bi-SQUID is one of the alternative solutions. Instead of the conventional DC SQUID, Bi-SQUID is designed by adding a parallel Josephson junction to typical DC SQUID. Bi-SQUID ‘s voltage response against external applied magnetic field is more linear than DC SQUID. [2], [3]

External applied magnetic field response of Bi-SQUID characterized by set of differential equations, there is no easy analytic way to solve these equations. [2], [4]Therefore, numerical analysis plays critical role for this type of systems. Modelling and simulation tools can support design studies by using numerical methods. However, there is no viable modelling and simulation application exist for Bi-SQUIDs.

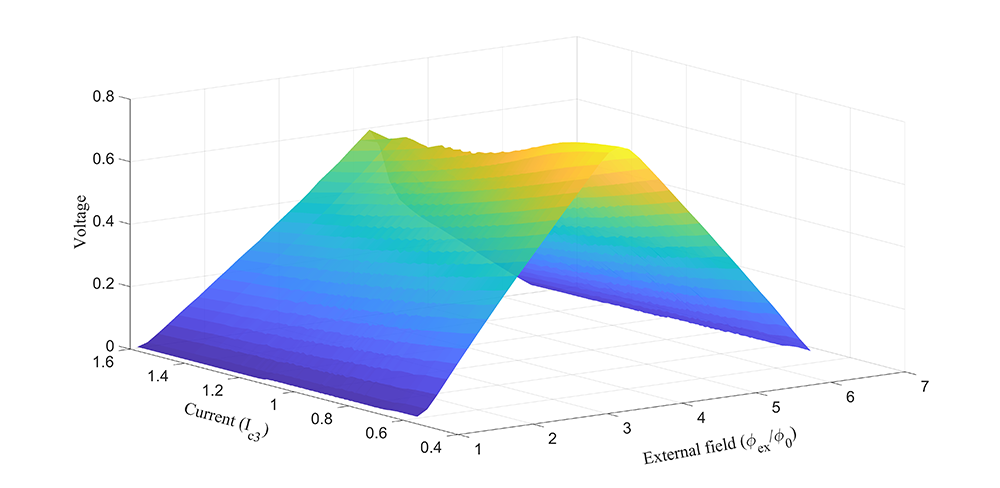
We developed an open-source and user-friendly statistical analysis tool for symmetric Bi-SQUIDs. Our simulation tool solves systems of differential equations. These equations represent Bi-SQUIDs system, the boundary conditions such as time step and external magnetic field data range can be defined by user. Our methodology is based on finding the voltage response of the symmetric Bi-SQUID for each time steps in the period. Our software gives the average voltage response of symmetric Bi-SQUID for each corresponding normalized applied external magnetic flux as an output. The normalized applied external magnetic flux range can be determined by the user. Moreover, our simulation tool provides multiple runs for the statistical analysis of Bi-SQUID. Users can determine margin and data range for one of the input parameters, and the tool generates gaussian distributed random numbers in a specific margin and data range for the said parameter. After that, the voltage response in an external applied magnetic field is achieved in the defined margin. These output sets, provide a wide range of design options to the user who can easily observe a reliable working range of Bi-SQUID circuits and can optimize Bi-SQUID design problems by using this output dataset. The figure represents visualized an example of output data of PySQUID. This figure shows the normalized voltage response of a Bi-SQUID with respect to variable normalized shunt junction current.

Acknowledgement
The authors want to thank Dr. Pascal Febvre from Université Savoie Mont Blanc, IMEP-LAHC, CNRS UMR5130, 73376 Le Bourget du Lac, France for his valuable guidance toward this work.

References
[1] R. L. Fagaly, ‘Superconducting quantum interference device instruments and applications’, Review of Scientific Instruments, vol. 77, no. 10, p. 101101, Oct. 2006, doi: 10.1063/1.2354545.
[2] V. K. Kornev, I. I. Soloviev, N. V. Klenov, and O. A. Mukhanov, ‘Bi-SQUID: a novel linearization method for dc SQUID voltage response’, Supercond. Sci. Technol., vol. 22, no. 11, p. 114011, Oct. 2009, doi: 10.1088/0953-2048/22/11/114011.
[3] V. K. Kornev, N. V. Kolotinskiy, and O. A. Mukhanov, ‘Bi-SQUID: design for applications’, Supercond. Sci. Technol., vol. 33, no. 11, p. 113001, Nov. 2020, doi: 10.1088/1361-6668/aba541.
[4] P. Longhini et al., ‘Voltage Response of Non-Uniform Arrays of Bi-SQUIDs’, in International Conference on Theory and Application in Nonlinear Dynamics (ICAND 2012), V. In, A. Palacios, and P. Longhini, Eds. Cham: Springer International Publishing, 2014, pp. 77–90. doi: 10.1007/978-3-319-02925-2_7.

Keywords: Bi-SQUID, SQUID, Analysis, Simulation