Topological insulator Bi₂Se₃ becomes topological superconductors by doping Cu or Sr [1,2]. These materials attract much interest because of the nematic state showing two-fold symmetry when magnetic field is applied parallel to ab-plane [3,4]. Although in-plane magnetic-field-angle dependence of resistivity has been measured to confirm nematicity, there had been only a few measurements of out-of-plane anisotropy. Out-of-plane anisotropy is also important because it represents dimensionality of superconductivity. Out-of-plane angle dependence of upper critical field (H_c2) is predicted by Tinkham model for 2D superconductivity and by anisotropic GL model for 3D. It is interesting which can be applied to doped Bi₂Se₃ because it has a layered crystal structure consisting of Bi-Se quintuple layers, which are bonded by van der Waals force.

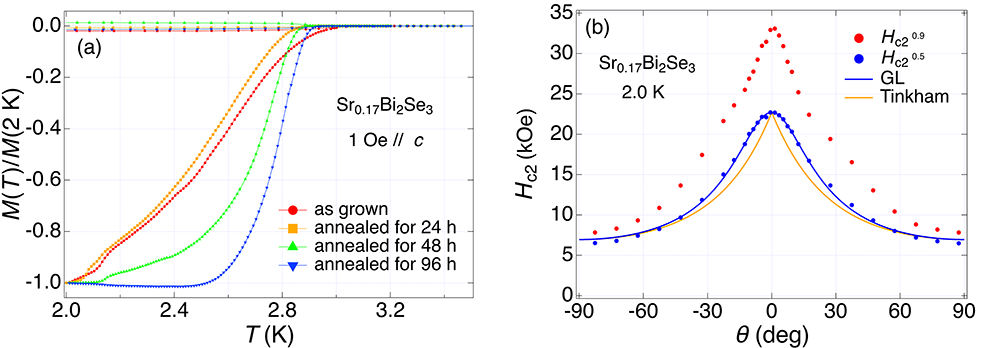
In this study, single crystals of Sr_xBi₂Se₃ (0.1 ≦ x≦ 0.3) were made by the flux method. Since it is known that obtaining high-quality crystals with sharp transition width is difficult due to large inhomogeneity [5], we tried various temperature conditions to improve the quality of the crystal. Single crystals were grown by slow cooling from the maximum temperature 1,000 ℃ and quenched at 650 ℃ or 700 ℃. In addition, one of the samples was prepared by furnace cooling. The transition width of the sample obtained by furnace cooling was the sharpest among all the crystals and it became even sharper by additional annealing as shown in Fig. 1(a).

Using these high-quality single crystals, out-of-plane magnetic-field-angle dependence of resistivity was measured. The obtained results are as follows: H_c2^ab = 2.2 T, H_c2^c = 0.65 T, γ = 3.3 (values at 2.0 K). The angle dependence of H_c2 shown in Fig. 1(b) is well fitted by the anisotropic GL model rather than the Tinkham model.

We will also discuss Hall resistivity and magnetoresistance in Sr_xBi₂Se₃.

Fig. 1(a): Temperature dependence of normalized magnetization in Sr_0.17Bi₂Se₃ obtained by furnace cooling followed by annealing at 560 ℃. (b) Out-of-plane magnetic-field-angle dependence of H_c2. θ = ±90° corresponds to c-axis. H_c2^0.9 is defined by ρ = ρ₀ + 0.9 (ρ_n - ρ₀) and H_c2^0.5 by ρ = ρ₀ + 0.5 (ρ_n - ρ₀). ρ₀ is residual resistivity and ρ_n is resistivity in the normal state.

[1] Y. S. Hor et al., Phys. Rev. Lett. 104, 057001 (2010).
[2] Z . Liu, et al. J. Am. Chem. Soc. 137, 10512 (2015).
[3] K. Matano et al., Nat. Phys. 12, 852 (2016).
[4] Y. Pan et al., Sci. Rep. 6, 28632 (2016).
[5] J. A. Schneeloch et al., Phys. Rev. B 91, 144506 (2015).

Keywords: topological superconductor, nematic superconductor, Bi2Se3, electrical transport properties