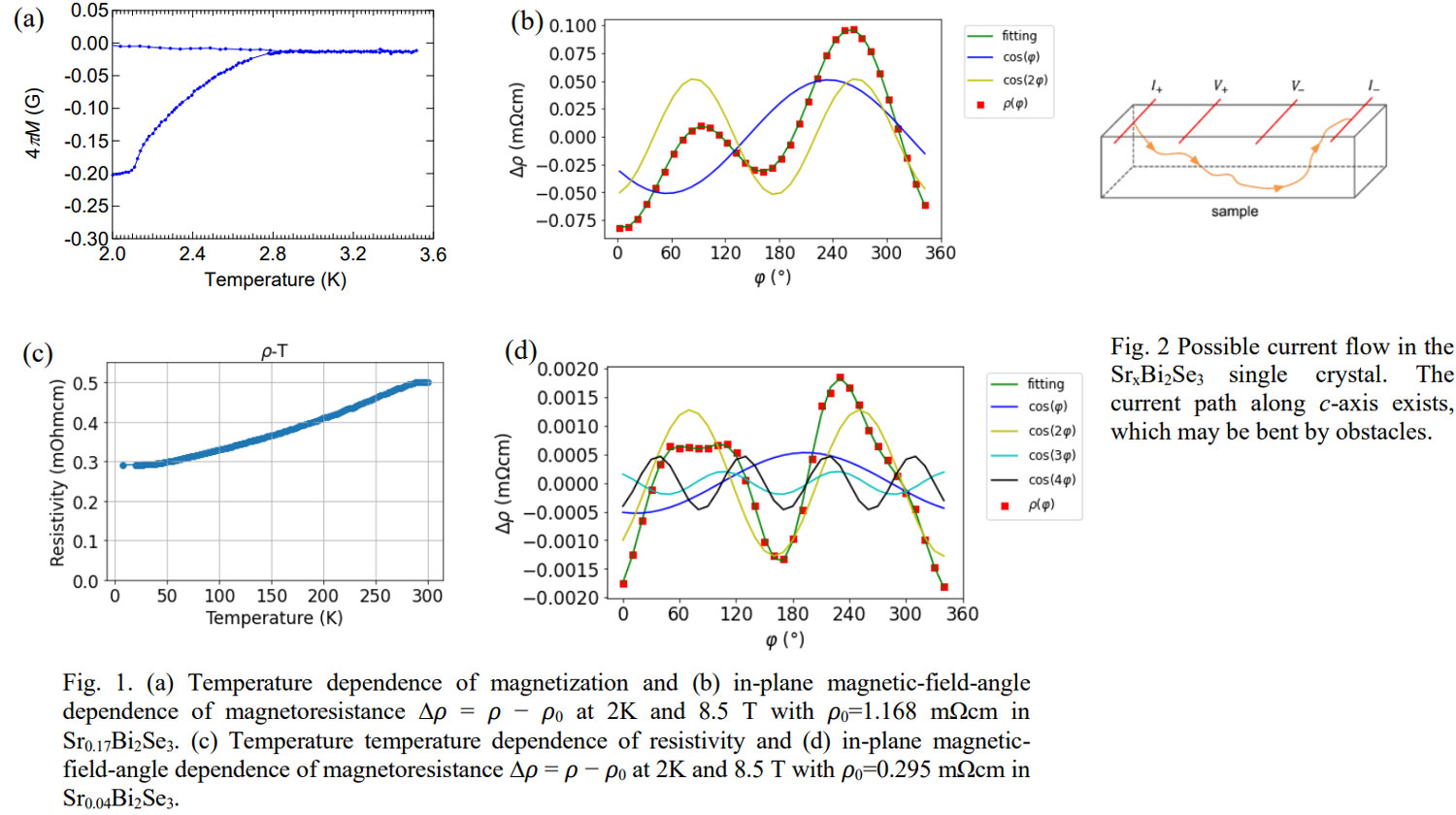
Bi₂Se₃ is one of the representative topological insulators that show unique metallic surface state despite their insulating nature of the bulk. By doping Cu or Sr into Bi₂Se₃, it becomes a topological superconductor, which shows novel properties such as nematicity [1]. In this study, we prepared high-quality single crystals of Sr_xBi₂Se₃ and investigated its in-plane magnetic-field-angle dependence of resistivity. Resistivity (ρ) was measured with current along a-axis at 2 K by applying the in-plane magnetic field along the direction at an angle φ from a-axis. We have measured samples with nominal compositions x = 0.04 and 0.17. Figures 1(a) and (c) show temperature dependences of magnetization in Sr_0.17Bi₂Se₃ and resistivity in Sr_0.04Bi₂Se₃, respectively, which show that sample with x = 0.17 is a superconductor with T_c = 2.8 K. Figures 1(b) and (d) show Δρ as a function of φ at 8.5 T, which is defined by Δρ ≡ ρ - ρ₀. Δρ(φ) mainly shows two-fold symmetry, or in other words nematicity. In Fig. 1(c), we also plot a fitting curve of Δρ(φ) with Δρ(φ) = ρ₁cos(φ + α₁) + ρ₂cos(2φ + α₂), where the 2nd term originates from the nematicity, magnetoresistance, or misalignment of the field from the in-plane direction. The fact that the minimum value of the 2φ component is at φ = 0^o strongly suggest that it is caused either by nematicity or by magnetoresistance. In the case of magnetoresistance, its magnitude should be proportional to the square of the transverse component of the field with respect to the current, (Bsin(φ))², which means that it is proportional to cos(2φ). One of the possible origins of the 1st term is the Hall effect for currents flowing along the c-axis as shown in Fig. 2. If this interpretation is correct, the Hall voltage should be zero at φ = 0^o and p. However, the zero-value angle is offset by ~-35^o as shown in Fig. 1(b). Such a shift can be explained by the shift of effective locations of the two voltage terminals, V₊ and V·_-. Namely, if locations of the effective voltage terminals are not parallel to a-axis, the zero-value position of the Hall effect should change. Fitting of Δρ(φ) of the sample with x = 0.04 with only cos(φ) and cos(2φ) terms was unsatisfactory. Instead, fitting with additional terms as Δρ(φ) = ρ₁cos(φ + α₁) + ρ₂cos(2φ + α₂) +ρ₃cos(3φ + α₃) + ρ₄cos(4φ + α₄) gave satisfactory result. However, physical origins of the 3rd and 4th terms are not clear at the present stage. The unusual Hall voltage due to current inhomogeneity may not have relationship with the superconductivity of Sr_xBi₂Se₃, because even non-superconducting Sr_xBi₂Se₃ with small x shows it. However, as x decreases, the amplitude of cos(φ) term decreases (Sr_0.17Bi₂Se₃: 8%, Sr_0.04Bi₂Se₃: 0.3%), which implies that there can be a critical value of x above which cos(φ) term appears. Samples with even smaller x will be measured to find the critical x value below which the cos(φ) term disappears and we will try to find out the possible physical origins of cos(3φ) and cos(4φ) terms by analyzing data on different samples at different temperatures and magnetic fields.

[1] Y. Pan et al., Sci. Rep. 6, 28632 (2016).
 Fig. 1. (a) Temperature dependence of magnetization and (b) in-plane magnetic-field-angle dependence of magnetoresistance ∆? = ? − ?₀ at 2K and 8.5 T with ?₀=1.168 mΩcm in Sr_0.17Bi₂Se₃. (c) Temperature temperature dependence of resistivity and (d) in-plane magnetic-field-angle dependence of magnetoresistance ∆? = ? − ?₀ at 2K and 8.5 T with ?₀=0.295 mΩcm in Sr_0.04Bi₂Se₃.
 Fig. 2 Possible current flow in the Sr_xBi₂Se₃ single crystal. The current path along c-axis exists, which may be bent by obstacles.

Keywords: SrxBi2Se3, topological superconductor, magneto-transport