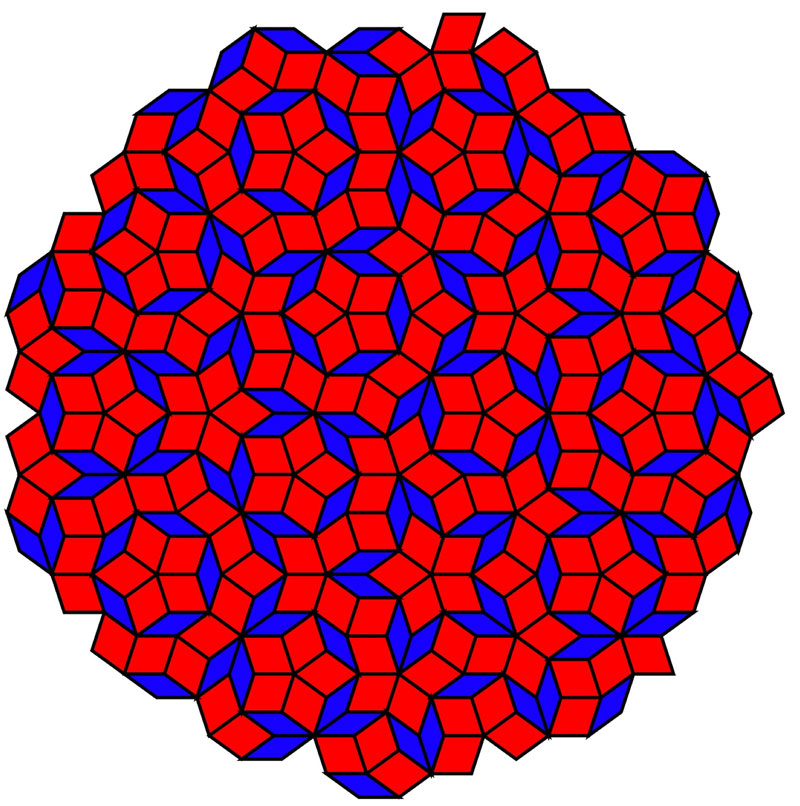
Symmetry-based analyses play an important role in the theory of topological superconductivity (TSC). In this regard, the effects of the symmetry of lattice structures on TSC provide our better understanding of TSC. Among various lattice structures, quasicrystals (QCs) have unique symmetry such as the five-fold rotational symmetry, which is forbidden in periodic lattices. TSC in two-dimensional quasicrystals has been investigated [1,2], where an s-wave TSC is realized in a Penrose tiling illustrated in Fig. 1. In the Penrose tiling, there are two sublattices that we denote A/B-sublattice. In the previous studies [1,2], it is assumed that the A- and B-sublattices have the same on-site potential. In real materials, however, such an assumption may not always be satisfied due to different local environments of sites in respective sublattices. Accordingly, we need to clarify the effect of bipartite lattice on TSC in quasicrystals.
In this study, we perform self-consistent calculation on the attractive Hubbard model with Zeeman field and Rashba spin-orbit coupling in a Penrose lattice. We introduce an on-site potential acting on A-sublattice sites, making A-sublattice and B-sublattice inequivalent. By changing the on-site potential, we calculate the topological invariant to classify the topology of the system. We find that topological phase transitions occur even in the presence of the on-site potential. We have thus confirmed that TSC can exist even when A-sublattice and B-sublattice are not equivalent in quasicrystals.

References:
[1] R. Ghadimi, T. Sugimoto, K. Tanaka, T. Tohyama, Phys. Rev. B 104, 144511 (2021).
[2] M. Hori et al., to be submitted.

Figure Caption:
Fig. 1. Penrose QCs.

Keywords: Topological superconductivity, Quasicrystals, Penrose tiling, Bipartite